A = π r 2. . A central angle in a circle is formed by two radii. This angle lets us define a portion of the circle’s circumference (an arc) or a portion of the circle’s area (a sector ). A central angle in a circle defines the area of a sector and the length of an arc. The number of degrees of arc in a circle is 360 .
TikTok Performance Benchmarks and Insights | Socialinsider
Sep 16, 2022Letting and in Equation 4.2.1, we get: θ = s r = 2 5 = 0.4 rad. In degrees, the angle is: θ = 0.4 rad = 180 π ⋅ 0.4 = 22.92 ∘. For central angles θ > 2π rad, i.e. θ > 360 ∘, it may not be clear what is meant by the intercepted arc, since the angle is larger than one revolution and hence “wraps around” the circle more than once.

Source Image: homework.study.com
Download Image
That’s what we’re going to try to solve for. We know that the central angle is 10 degrees. So you have 10 degrees over 360 degrees. So we could simplify this by multiplying both sides by 18 pi. And we get that our arc length is equal to– well, 10/360 is the same thing as 1/36. So it’s equal to 1/36 times 18 pi, so it’s 18 pi over 36, which is

Source Image: chegg.com
Download Image
Find the length of s and area A. | Homework.Study.com
Question Transcribed Image Text: Use the given circle. Find the length s to the nearest tenth. 9 in. O47.1 in. O 23.6 in. O 56.5 in. Expert Solution Trending now This is a popular solution! Step by step Solved in 2 steps See solution Check out a sample Q&A here Knowledge Booster Learn more about Area of a Circle

Source Image: zapier.com
Download Image
Use The Given Circle Find The Length Of S
Question Transcribed Image Text: Use the given circle. Find the length s to the nearest tenth. 9 in. O47.1 in. O 23.6 in. O 56.5 in. Expert Solution Trending now This is a popular solution! Step by step Solved in 2 steps See solution Check out a sample Q&A here Knowledge Booster Learn more about Area of a Circle
ISBN: 9781337798310. Author: Peterson, John. Publisher: Cengage Learning, Solution for Use the given circle. Find the length s to the nearest tenth. 3 m 12.6 m 6.3 m 3.1 m O d 2.0 m.
The 6 best free email marketing services in 2024 | Zapier
Calculus Sufy M. asked • 08/04/20 Find the length s of the circular arc. Find the length s of the circular arc. (Assume r = 6 and θ = 110°.) s = Follow • 1 Add comment Report 2 Answers By Expert Tutors Best Newest Oldest Nitai M. answered • 08/04/20 Tutor 5.0 (51) Dedicated Tutor for MCAT, Bio/Chem/Physics, and USMLE About this tutor ›
SOLVED: 38. Use the given circle. Find the length s to the nearest tenth. 15.7 in. 37.7 in. 31.4 in. 18.8 in.
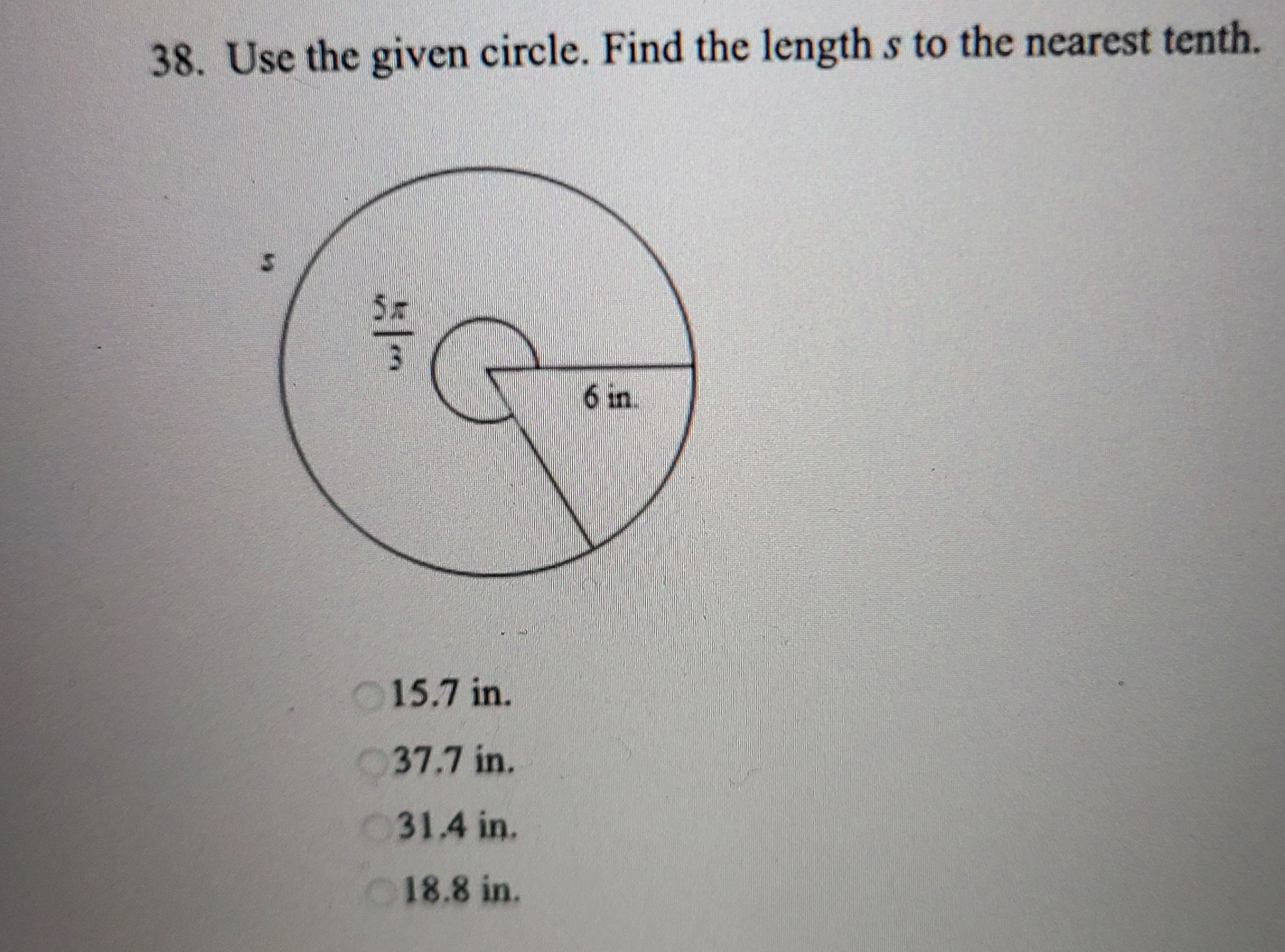
Source Image: numerade.com
Download Image
1. Use the given circle. Find the length s to the nearest tenth A. 3.1 in. B. 15.7 in. C. 31.4 in. – brainly.com
Calculus Sufy M. asked • 08/04/20 Find the length s of the circular arc. Find the length s of the circular arc. (Assume r = 6 and θ = 110°.) s = Follow • 1 Add comment Report 2 Answers By Expert Tutors Best Newest Oldest Nitai M. answered • 08/04/20 Tutor 5.0 (51) Dedicated Tutor for MCAT, Bio/Chem/Physics, and USMLE About this tutor ›

Source Image: brainly.com
Download Image
TikTok Performance Benchmarks and Insights | Socialinsider
A = π r 2. . A central angle in a circle is formed by two radii. This angle lets us define a portion of the circle’s circumference (an arc) or a portion of the circle’s area (a sector ). A central angle in a circle defines the area of a sector and the length of an arc. The number of degrees of arc in a circle is 360 .
Source Image: socialinsider.io
Download Image
Find the length of s and area A. | Homework.Study.com
That’s what we’re going to try to solve for. We know that the central angle is 10 degrees. So you have 10 degrees over 360 degrees. So we could simplify this by multiplying both sides by 18 pi. And we get that our arc length is equal to– well, 10/360 is the same thing as 1/36. So it’s equal to 1/36 times 18 pi, so it’s 18 pi over 36, which is

Source Image: homework.study.com
Download Image
Arc Length – GCSE Maths – Steps, Examples & Worksheet
Formula for S = rθ S = r θ. The picture below illustrates the relationship between the radius, and the central angle in radians. The formula is S = rθ S = r θ where s represents the arc length, S = rθ S = r θ represents the central angle in radians and r is the length of the radius.

Source Image: thirdspacelearning.com
Download Image
Next-generation AI on the frontline with Microsoft Teams | Microsoft 365 Blog
Question Transcribed Image Text: Use the given circle. Find the length s to the nearest tenth. 9 in. O47.1 in. O 23.6 in. O 56.5 in. Expert Solution Trending now This is a popular solution! Step by step Solved in 2 steps See solution Check out a sample Q&A here Knowledge Booster Learn more about Area of a Circle

Source Image: microsoft.com
Download Image
What are Load Cells and How Do They Work?
ISBN: 9781337798310. Author: Peterson, John. Publisher: Cengage Learning, Solution for Use the given circle. Find the length s to the nearest tenth. 3 m 12.6 m 6.3 m 3.1 m O d 2.0 m.

Source Image: omega.com
Download Image
1. Use the given circle. Find the length s to the nearest tenth A. 3.1 in. B. 15.7 in. C. 31.4 in. – brainly.com
What are Load Cells and How Do They Work?
Sep 16, 2022Letting and in Equation 4.2.1, we get: θ = s r = 2 5 = 0.4 rad. In degrees, the angle is: θ = 0.4 rad = 180 π ⋅ 0.4 = 22.92 ∘. For central angles θ > 2π rad, i.e. θ > 360 ∘, it may not be clear what is meant by the intercepted arc, since the angle is larger than one revolution and hence “wraps around” the circle more than once.
Find the length of s and area A. | Homework.Study.com Next-generation AI on the frontline with Microsoft Teams | Microsoft 365 Blog
Formula for S = rθ S = r θ. The picture below illustrates the relationship between the radius, and the central angle in radians. The formula is S = rθ S = r θ where s represents the arc length, S = rθ S = r θ represents the central angle in radians and r is the length of the radius.